Polya sanab chiqish teoremasi - Pólya enumeration theorem
The Polya sanab chiqish teoremasi, deb ham tanilgan Redfild - Polya teoremasi va Polya hisoblash, bu teorema kombinatorika ikkalasi ham kelib chiqadi va oxir-oqibat umumlashtiradi Burnside lemmasi soni bo'yicha orbitalar a guruh harakati a o'rnatilgan. Teorema birinchi marta tomonidan nashr etilgan J. Xovard Redfild 1927 yilda. 1937 yilda u tomonidan mustaqil ravishda qayta kashf etilgan Jorj Polya, natijada natijani ko'plab hisoblash muammolariga, xususan, sanab chiqishda qo'llash orqali natijani juda ommalashtirdi kimyoviy birikmalar.
Polya sanab chiqish teoremasi kiritilgan ramziy kombinatorika va nazariyasi kombinatorial turlar.
Soddalashtirilgan, vaznsiz versiyasi
Ruxsat bering X bo'lishi a cheklangan to'plam va ruxsat bering G bo'lishi a guruh ning almashtirishlar ning X (yoki a cheklangan simmetriya guruhi bu harakat qiladi kuni X). To'plam X sonli boncuklar to'plamini anglatishi mumkin va G boncukların tanlangan permütasyonlar guruhi bo'lishi mumkin. Masalan, agar X a marjon ning n doira ichida boncuklar, keyin aylanish simmetriyasi dolzarbdir G bo'ladi tsiklik guruh Cn, agar bo'lsa X a bilaguzuk ning n doira ichida boncuklar, aylanishlar va aks ettirishlar dolzarbdir G bo'ladi dihedral guruh D.n 2-tartibn. Yana shuni aytaylik Y munchoqlarning ranglari - shuning uchun cheklangan ranglar to'plami YX bu boncukların rangli tartiblari to'plami (rasmiy ravishda: YX funktsiyalar to'plamidir .) Keyin guruh G harakat qiladi YX. Polya sanab chiqish teoremasi ostidagi orbitalar sonini hisoblaydi G boncukların rangli formulalari quyidagi formula bo'yicha:
qayerda ranglarning soni va v(g) ning soni tsikllar guruh elementining g ning permutatsiyasi sifatida qaralganda X.
To'liq, vaznli versiya
Teoremaning umumiyroq va muhimroq versiyasida ranglar ham bir yoki bir nechta usullar bilan tortiladi va ranglar to'plamida cheksiz ko'p ranglar bo'lishi mumkin. ishlab chiqarish funktsiyasi cheklangan koeffitsientlar bilan. Bitta o'zgaruvchan holda, deylik
ranglar to'plamining yaratuvchi funktsiyasi bo'lib, ular mavjud fw vazn ranglari w har biriga tamsayı w ≥ 0. Ko'p o'zgaruvchan holatda har bir rangning vazni butun sonlarning vektoridir va hosil qiluvchi funktsiya mavjud f(t1, t2, ...) har bir berilgan og'irlik vektori bilan ranglar sonini jadvalga kiritadigan.
Sanab chiqish teoremasida yana bir ko'p o'zgaruvchan ishlab chiqarish funktsiyasi qo'llaniladi tsikl indeksi:
qayerda n ning elementlari soni X va vk(g) ning soni k- guruh elementining tsikllari g o'rnini bosuvchi sifatida X.
Rangli tartib - bu harakatning orbitasi G to'plamda 'YX (qayerda Y ranglar to'plami va YX barcha funktsiyalar to'plamini bildiradi φ: X→Y). The vazn Bunday tartibning og'irliklari yig'indisi sifatida belgilanadi φ (x) hamma ustidan x yilda X. Teorema ishlab chiqaruvchi funktsiya deb ta'kidlaydi F og'irlik bo'yicha rangli tartib sonining soni quyidagicha:
yoki ko'p o'zgaruvchan holatda:
Agar mavjud bo'lsa, ilgari berilgan soddalashtirilgan versiyaga qisqartirish uchun m ranglar va barchasi 0 ga teng, keyin f(t) = m va
Sanab o'tilgan daraxtlarni (pastroqqa qarang) va asiklik molekulalarni nishonlashda "rangli munchoqlar" ning joylashishi aslida ildiz otgan daraxt shoxlari kabi tartiblardir. Shunday qilib ishlab chiqarish funktsiyasi f chunki ranglar ishlab chiqarish funktsiyasidan kelib chiqadi F kelishuvlar uchun va Polya sanoq teoremasi rekursiv formulaga aylanadi.
Misollar
Marjonlarni va bilakuzuklar
Rangli kublar
Uch o'lchovli kub tomonlarini bo'yashning qancha usullari mavjud m ranglar, kubning aylanishigacha? Aylanish guruhi C kubning boncuklarga teng bo'lgan oltita tomonida harakat qiladi. Uning tsikl indeksi
ning har 24 elementining harakatini tahlil qilish natijasida olinadi C kubning 6 tomonida, qarang Bu yerga tafsilotlar uchun.
Biz 0 rangga ega bo'lish uchun barcha ranglarni olamiz va ularning mavjudligini aniqlaymiz
turli xil ranglar.
Uch va to'rtta tepalikdagi grafikalar
Grafik yoqilgan m tepaliklarni rangli boncuklar qatori sifatida talqin qilish mumkin. To'plam X "boncuklar" ning to'plami ranglar to'plami esa mumkin qirralar Y = {qora, oq} qirralarga to'g'ri keladi (qora) yoki yo'q (oq). Grafik sonini hisoblashda Polya sanoq teoremasidan foydalanish mumkin qadar izomorfizm belgilangan vertikal sonlar bilan yoki ushbu grafalarni ularning chekkalari soniga qarab hosil qiluvchi funktsiya bilan. Ikkinchi maqsad uchun aytishimiz mumkinki, qora yoki hozirgi chekka 1 vaznga ega, yo'q yoki oq chekka 0 vaznga ega. ranglar to'plami uchun ishlab chiqaruvchi funktsiya. Tegishli simmetriya guruhi The nosimmetrik guruh kuni m harflar. Ushbu guruh to'plamda ishlaydi X mumkin qirralarning: permutatsiya φ {a, b} chekkasini {φ (a), φ (b)} chetga aylantiradi. Ushbu ta'riflar bilan grafiklarning izomorfizm sinfi m tepaliklar harakatining orbitasi bilan bir xil G to'plamda YX rangli kompozitsiyalar; grafik qirralarning soni tartibning og'irligiga teng.

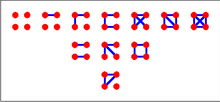
Uchta tepadagi sakkizta grafik (izomorfik grafikalarni aniqlashdan oldin) o'ng tomonda ko'rsatilgan. Graflarning to'rtta izomorfizm klassi mavjud, ular o'ng tomonda ham ko'rsatilgan.
Guruhning tsikl ko'rsatkichi S3 uchta qirralarning to'plamida harakat qilish
(guruh elementlari harakatining tsikl tuzilishini tekshirish natijasida olingan; qarang Bu yerga ). Shunday qilib, sanoq teoremasiga ko'ra, izomorfizmgacha bo'lgan 3 ta tepalikdagi grafiklarning hosil bo'lish funktsiyasi
bu soddalashtiradi
Shunday qilib, har biri 0 dan 3 tagacha bo'lgan bitta grafik mavjud.
Guruhning tsikl ko'rsatkichi S4 6 qirralarning to'plamida harakat qilish
(qarang Bu yerga.) Shuning uchun
bu soddalashtiradi
Ushbu grafikalar o'ng tomonda ko'rsatilgan.
Ildiz daraxtlari
To'plam T3 ildizli uchlamchi daraxtlar har bir tugunda (yoki bargsiz tepada) to'liq uchta farzand (barg yoki subtree) bo'lgan ildiz otgan daraxtlardan iborat. Kichik uchlik daraxtlari o'ng tomonda ko'rsatilgan. Bilan ildiz otgan uchlik daraxtlarini unutmang n tugunlari bilan ildiz otgan daraxtlarga teng n eng yuqori daraja 3 (barglarni e'tiborsiz qoldirib). Umuman olganda, ikkita ildiz otgan daraxt izomorfikdir, chunki ikkinchisidan uning tugunlari bolalarini bosib olish mumkin. Boshqacha qilib aytganda, tugunning bolalariga ta'sir qiluvchi guruh nosimmetrik guruhdir S3. Biz bunday uchlik daraxtining vaznini tugunlar soni (yoki bargsiz tepaliklar) sifatida aniqlaymiz.

Ildizlangan uchlamchi daraxtni rekursiv ob'ekt sifatida ko'rish mumkin, bu barg yoki o'zlari ildiz otgan daraxtlar bo'lgan uchta bolali tugun. Ushbu bolalar boncuklara teng; nosimmetrik guruhning tsikl ko'rsatkichi S3 ularga amal qiladigan narsa
Polya sanab chiqish teoremasi ildiz otgan uchlik daraxtlarining rekursiv tuzilishini tugunlar soni bo'yicha ildiz otilgan uchlik daraxtlarining F (t) hosil qilish funktsional tenglamasiga aylantiradi. Bunga uchta bolani tugun raqami bo'yicha tortilgan, ildiz otilgan uchlik daraxtlari bilan "rang berish" orqali erishiladi, natijada rang hosil qilish funktsiyasi quyidagicha beriladi. sanab chiqish teoremasi beradi
tugun sonidan bitta kichik vaznga ega bo'lgan ildiz otilgan daraxtlar uchun hosil qiluvchi funktsiya sifatida (chunki bolalar og'irliklari yig'indisi bu hisobga olinmaydi).
Bu raqamning quyidagi takrorlanish formulasiga tengdir tn bilan ildiz otgan uchlik daraxtlari n tugunlar:
qayerda a, b va v manfiy bo'lmagan butun sonlardir.
Ning dastlabki bir nechta qiymati bor
- 1, 1, 1, 2, 4, 8, 17, 39, 89, 211, 507, 1238, 3057, 7639, 19241 (ketma-ketlik) A000598 ichida OEIS )
Teoremaning isboti
Polya sanab chiqish teoremasining soddalashtirilgan shakli quyidagilardan kelib chiqadi Burnside lemmasi, bu ranglarning orbitalari soni ning elementlari sonining o'rtacha ekanligini aytadi almashtirish bilan belgilanadi g ning G barcha almashtirishlar ustida g. Teoremaning vaznli versiyasi aslida bir xil dalilga ega, ammo Burnside lemmasining aniq sanab o'tilgan shakli bilan. Burnside lemmasini har xil og'irlikdagi orbitalarga alohida qo'llash tengdir.
Aniqroq belgilash uchun ruxsat bering ishlab chiqaruvchi funktsiyaning o'zgaruvchilari bo'ling f ning . Og'irliklar vektori berilgan , ruxsat bering ning mos monomial muddatini belgilang f. Burnside lemmasini vazn orbitalariga qo'llash , bu vaznning orbitalari soni
qayerda vaznning rang berish to'plamidir ular tomonidan belgilanadi g. Agar biz barcha mumkin bo'lgan og'irliklarni yig'sak, biz olamiz
Ayni paytda guruh elementi g tsikl tuzilishi bilan muddatga hissa qo'shadi
ning tsikl indeksiga G. Element g elementni tuzatadi agar va faqat funktsiya har bir tsiklda doimiy bo'lsa q ning g. Har bir bunday tsikl uchun q, | ning og'irligi bo'yicha hosil qiluvchi funktsiyaq| tomonidan sanab o'tilgan to'plamdan bir xil ranglar f bu
Bundan kelib chiqadiki, nuqtalarning og'irligi bo'yicha hosil qiluvchi funktsiya bilan belgilanadi g ning barcha tsikllari bo'yicha yuqoridagi muddatning hosilasi g, ya'ni
Buning o'rniga, barchasini yig'indisiga qo'ying g da'vo qilinganidek, almashtirilgan tsikl indeksini beradi.
Adabiyotlar
- Redfild, J. Xovard (1927). "Guruh tomonidan qisqartirilgan taqsimot nazariyasi". Amerika matematika jurnali. 49 (3): 433–455. doi:10.2307/2370675. JSTOR 2370675. JANOB 1506633.
- Frank Xarari; Ed Palmer (1967). "Redfildni sanash usullari". Amerika matematika jurnali. 89 (2): 373–384. doi:10.2307/2373127. JSTOR 2373127. JANOB 0214487.
- G. Polya (1937). "Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen". Acta Mathematica. 68 (1): 145–254. doi:10.1007 / BF02546665.
- G. Polya; R. C. O'qing (1987). Guruhlar, grafikalar va kimyoviy birikmalarni kombinatorial sanab chiqish. Nyu York: Springer-Verlag. ISBN 0-387-96413-4. JANOB 0884155.
Tashqi havolalar
- Polya-Burnside sanab chiqish teoremasini qo'llash Gektor Zenil va Oleksandr Pavlik tomonidan, Wolfram namoyishlari loyihasi.
- Vayshteyn, Erik V. "Polya sanab chiqish teoremasi". MathWorld.
- Frederik Chyzak Alkogollarni va kimyoviy molekulalarning boshqa sinflarini sanash, Polya nazariyasining namunasi.






































